Simulation of signal output with noise using signal generator
In real circuits, actual signals often contain noise. The noise problem has become an important factor to be considered in circuit design. Regardless of the power input, the propagation of the internal path of the circuit, and even the signal output of the signal, there are many noise problems that need to be overcome. The designer can simulate the noise output by the signal generator to judge the noise tolerance of the DUT.
For example, if a switch mode power supply (SMPS) is used in the output circuit of the power supply, the frequency of the technology adopted by the current switching power supply is often higher than 20kHz, in conjunction with pulse wave modulation (PWM) and the output of filter circuit can convert the city power into the DC voltage required by the IC circuit such as +5V, +12V, etc. However, the side effect after conversion is that there is a little AC component in the DC component. If the AC component (hereinafter referred to as noise) is too large, it will cause the application circuit to malfunction. Take 5V as an example. If the DC center voltage is 5.00V and the noise is 1.0 Vp-p, any transient voltage value may have exceeded the allowable range of 4.75V-5.25V (this is the normal operating voltage range of general logic ICs), which may malfunction or crash, so the impact of output noise is not small. Through this article, users can understand how to generate noise-containing output with signal generator simulation.
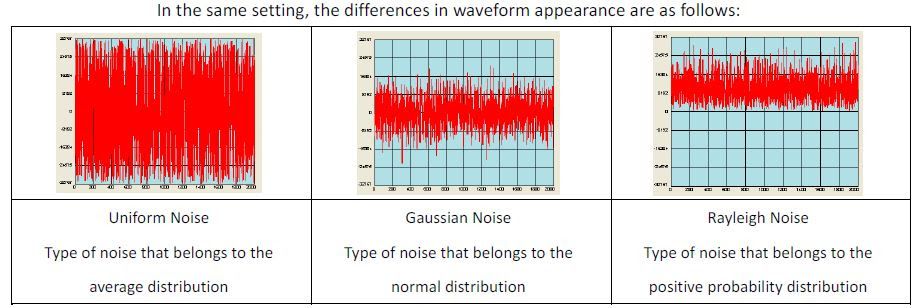
Take AFG-3000 as an example, it provides 8M long memory depth, which allows users to edit or output any number of points within the 8M range. It is also equipped with arbitrary waveform editing software, which can satisfy the need to generate noise-containing signal output. There are three types of noise built into the AFG-3000 arbitrary waveform editing software, namely Uniform Noise, Gaussian Noise and Rayleigh Noise. The main difference lies in the range of probability distribution.

For example, a 6Vpp/40kHz sine wave contains 200mVpp noise, and the result of adding noise can be displayed through the waveform calculation in the PC software of AFG-3000. The approaches are as follows:
1. First describe the 6Vpp/40kHz sine wave:
- In the number of points, select the total number of points to form the sine wave. This time it is set to 5000 points, and the frequency is set to 40,000 Hz (40 kHz).
- Since the amplitude representation of the PC software is directly calculated in 16bit points, the range +32,767 ~ -32,767 corresponds to 10Vpp (+5V ~ -5V), then:
+3V corresponds to 32,767/5V*3V = 19,660 (points);
-3V corresponds to -32,767/5V*3V = -19,660 (points)
The remaining parameters (such as points, frequency range, period, phase, etc.) can be set according to the required values.

2. Click the Cursor option in the toolbar at the top of the software, and use the mouse to select the area to be calculated.

3. Select Math(M) >> Add at the top of the toolbar
4. Select the waveform to be calculated. Here, take the average noise as an example (Uniform Noise); the average noise is about 200mVpp (+100mV ~ -100mV) amplitude, and its amplitude is about 32,767/5V*0.1V = 655(points) ~ -32767/5V*0.1V = -655 (points)
5. The result obtained after the calculation is shown in the figure, and a sine wave with noise will be obtained.
6. Save the edited file and upload it to AFG-3000 via USB Flash drive, and set its output range and amplitude (AMPL) on the instrument to 10Vpp.
7. Turn on the Main Output on the AFG-3000, send the edited signal to the oscilloscope, and you will find that the waveform curve after adding noise is obviously thicker than the original waveform.
The noise simulation application mentioned above is mainly for adding noise to the pure signal to simulate the actual transmission signal when designing the circuit to test the noise tolerance of the DUT. Such an application can be easily implemented by the AFG-3000.
Please contact us for further information of the AFG-3000 series.





